The Treasured Dark Skies of Florida’s Forgotten Coast 

We are excited to partner with local photographer and architect, Kathryn Stivers, to bring you a beautiful new art exhibit outside of our Planetarium theater. The exhibit, Treasured Dark Skies of Florida’s Forgotten Coast, highlights Stivers’ astro-landscape photography. This technique uses long exposure to capture earthly foregrounds against the backdrop of the cosmos.

See more of Kathryn’s work here: https://www.distantlightstudio.com/shop-art 

Exhibit Sponsored by Architects Lewis + Whitlock and Capital City Bank

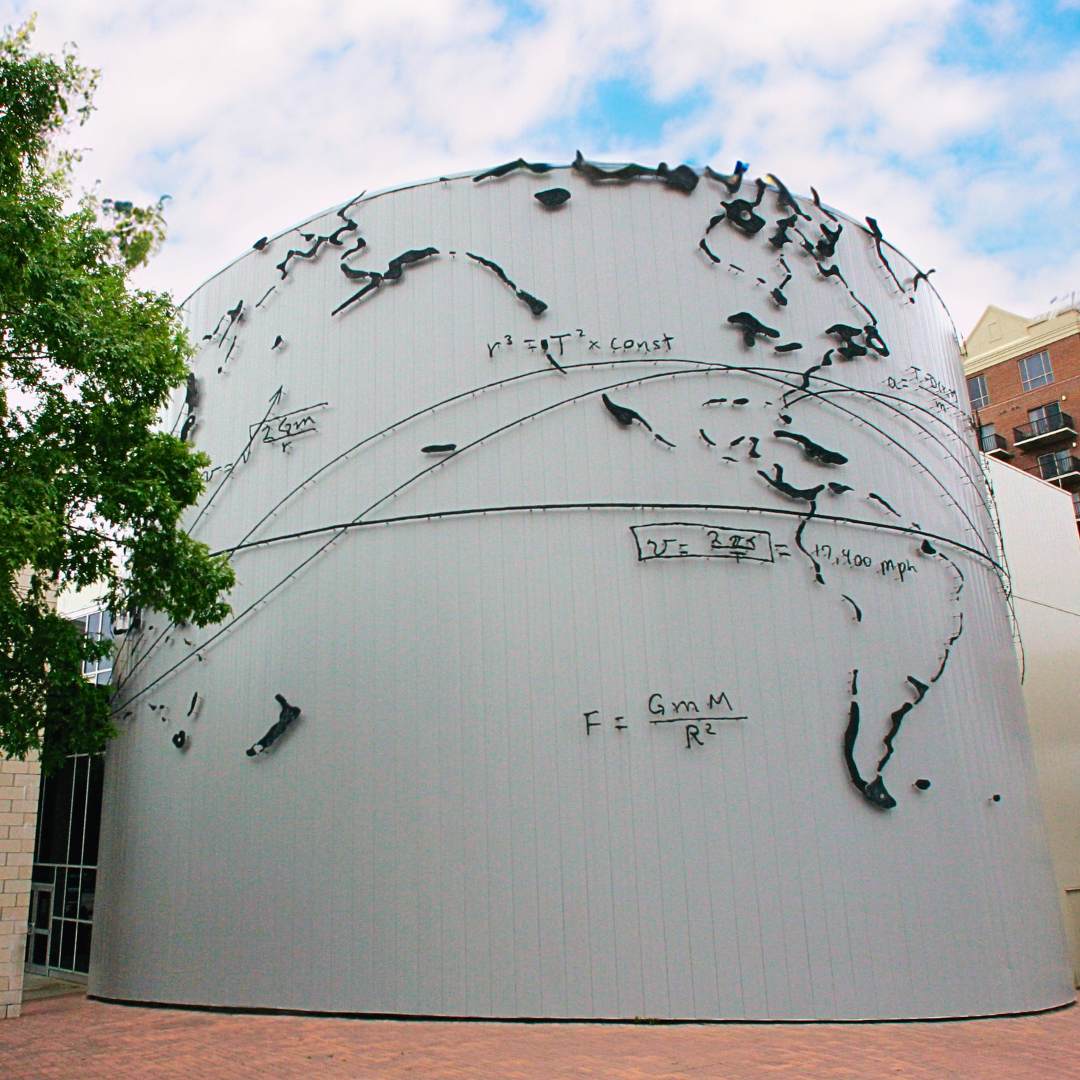
The Challenge of Space

The artwork, “The Challenge of Space” located on the outside of the Challenger Learning Center Planetarium was created by Gregory M. Gomez with funding from Florida’s Art in State Buildings Program. The work features 400 bronze cast elements designed to reflect the Earth’s land masses, rocket launch trajectories, and equations for calculating escape velocities and geosynchronous orbits.

Featured Equations:

Escape Velocity takes into account the mass of an object (m) and the radius of the surface of the planet (r), then by accelerating the object to the escape velocity (v) it will leave the gravitational field of the planet and continue out to infinity. The equation reads: v=2G m/r = 25,000 mph.

Force and Acceleration applies a force (F) to to any object of mass (m) and causes the object to accelerate (increase its velocity) at a value (a). F=m a, F = mR (Newton’s 2nd)

Force of Gravitation – Any two objects are attracted by a force (F) determined by the masses of the objects (m1 and m2) and the square of the distance between them (d2). I the distance of them is doubled, the force between them is one-quarter. F=G m1 m2 /d2.

Kepler’s 3rd Law – The period (T) of a satellite orbiting a planet is related to the radius of the orbit (r). r3 / T2=constant.

Acceleration caused by thrust – Given a constant thrust of a rocket (T) which has a mass (m), then it will attain an acceleration (a) when leaving the planet’s surface. a=(T-m g) / m (Goddard).

Orbiting Velocity – For any satellite orbiting a planet, the orbital period and the velocity depend only on the radius of the orbit. The International Space Station has an orbital period of 96.7 minutes and a velocity of 17,400 mph. v=2 pr/T

To see more public art in downtown Tallahassee take the downtown public art walk curated by the Council on Culture and Art at https://www.tallahasseearts.org/downtown-public-art-walk/.

Funding and sponsorship from the Council on Culture and Arts

Brief History of Space Exploration

In our dedication to honoring the milestones of space exploration and heralding the latest advancements, we present a curated timeline delving into a concise history of our ventures beyond Earth. Although not exhaustive, this timeline serves as an initial journey for students and families alike to witness the remarkable strides humanity has taken in our exploration of the cosmos.